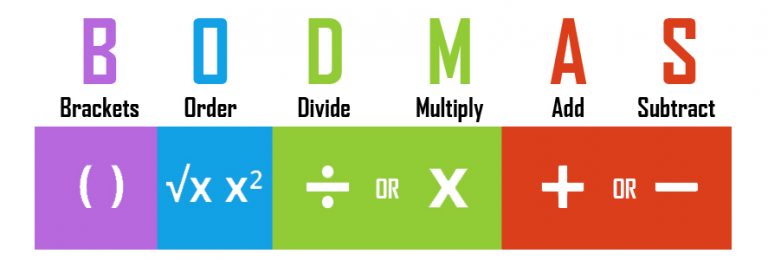
Lets understand a simple rule of BODMAS. Some call it as BIDMAS. In this case the "I" means Indices which is simply another word for 'order' or 'other' and the concept is exactly the same. This topicis one of the most important topic for 11 Plus exams for grammar schools and also maths as subject. Teacher at Champs Learning explains this topic with examples.

Understanding BODMAS:

Though this area may have less of direct questions appearing in most of the competitive exams, but its indirect application makes this topic very relevant from the maths section point of view. Simplification or simplify fractions means to simplify a complicated mathematical expression to get a single or direct answer.

To understand it clearly, let us solve the following example.

Illustration: Solve 12 + 8 ÷ 4

Sol: The correct solution is as follows = 12 + 8 ×(1/4) = 12 + 2 = 14

Note: Many students will solve it as follows: 12 + 8 ¸ 4 = 20 ÷ 4 = 5 which is wrong. We must follow the Bodmas formula. According to BODMAS rule, multiplication should be after division. Given below are the details of the letters and the sequence to be followed while solving simplification or BODMAS based questions.

BODMAS rule

B - Bracket (Brackets are solved in order of (), {} and [] respectively.

O - Of Þ multiplication, but it is to be done before division.

D - Division

M - Multiplication

A - Addition

S - Subtraction

So for simplifying expressions, we must follow the above sequence. In the previous given example, we first divide 8 by 4 and add it to 12 as division (D) is before multiple (M) in BODMAS.

Note: Remember to replace every division symbol with multiplication symbol followed by the reciprocal of the number following the division symbol, as shown in the above illustration. This simplification trick must be applied to simplify math problems.

Now let us solve a few examples to understand simplification in Maths. Besides that, you will also learn simplifying the algebraic expressions.

Please go through the following simplification questions

Level 01 Questions

Example 1: Solve: 10 + 10 × 10 ÷ 10.

Sol: Applying BODMAS rule: 10 + 10 × 10 × (1/10) ⇒ 10 +10 = 20

Example 2: 8 + 8 of 8 ÷ 8 - 34/5

Sol: 8 + 64 ÷ 8 - (34/5) (Note: ‘of’ must be solved before ‘÷’)

= 8 + 8 - (34/5) ⇒ 16 - (34/5) = 46/5

Example 3: Simplify the expression: 18 – [6 – {4 – (8 – 6 + 3 )}]

Sol: This is an example where brackets are given. Brackets are solved after Bar. The order of Solving the brackets is (), {} and [] respectively. So, the solution of above examples is as follows.

= 18 – [6 - {4 – (8 – 9)}] ⇒ 18 – [6 – {4 – (- 1)}]

= 18 – [6 - {4 + 1}] ⇒ 18 – [ 6 – 5] Þ 18 – [ 1] = 18 – 1 = 17

Example 4: Solve

20+20×20÷20/20×20÷+20

Sol: 20+20×20÷20/20×20÷+20 = 20+20×20×(1/2)/20×20×(1/20)+20

=20+20/20+20=40/40=1

Example 5: Simplify: 8÷8 of 8+8/8÷8×8+8

Sol: 8÷8 of 8+8/8÷8×8+8 ⇒ 8÷64+8/8×(1/8)×8+8

8×(1/64)+8/8+8 = (1/8)+8/16 ⇒ 65/8 × 1/16 = 65/128

Example 6: 3√125-√? = 3

>Sol: 5-√x =3

5 – 3 = √x

√x = 2 ⇒ x = 4.

Example 7: Solve; 30% of 300 + x % of 50 = 60% of 400.

Sol: 30% of 300 + x% of 50 = 60% of 400.

90 + (x/2) = 240

x/2 = 240 – 90

x/2 =150 ⇒ x = 150 2 =300

Example 8 : Solve; 6162 + ? + 3330 = 2545.

Sol: 6162 + x + 3330 = 2545

x = 2545 – 6162 – 3330 = 2545 – 9492 = - 6947.

Level 02 Questions

Solve the following simplification questions

Q.1.

5÷√5=?

A. √5 B. 5 C. 25 D. 0.05

Sol : Option B

Applying BODMAS rule: 5 ÷ √5 = 5/√5 = √5

Q.2.

Solve 5(1/2) + 6(1/2) - 8(1/4)A. 2(3/4) B. 3(3/4) C. 2(1/4) D. None of these

Sol : Option B

5(1/2) + 6(1/2) - 8(1/4) = (5+6-8) + ((1/2) + (1/2) - (1/4)) = 3(3/4)

Q.3.

22 – [9 – {6 – (10 –4-3 )}]

A.12 B. 14 C. 10 D. 8

Sol : Option C

22 – [9 – {6 – (10 –4-3 )}]

= 22 - [9 - {6 -) - (10 – 1)}] = 22 - [ 9 - { 6 - 9}]

= 22 - [9 - {-3}] = 22 - [9 + 3] = 22 - [12] = 22 - 12 = 10

Q.4.

103 - 33 - 23/102 =?

A. 9.5 B. 9.62 C. 9.61 D. 9.6

Sol : Option A

103 - 33 - 23/102

= 1000-27-8/100

=965/100 = 9.65

Q.5.

(14)2 – (.06)2194.36 B. 193.36 C. 195.36 D. None of these

Sol : Option D

(14)2 – (.06)2

= 196 - .0036 = 195 .9964

Q.6.

37.5% of 800 – 6.25% of 1600 =?

A. 200 B. 250 C. 275 D. 236

Sol : Option A

37.5% of 800 - 6.25% of 1600

3/8 × 800 - 1/16 × 1600 = 300 – 100 = 200

Q.7.

(√289/34) × (68/√1156) × (√961/62) = ?

A. ½ B. ¾ C. 5/6 D. 7/8

Sol : Option A

(√289/34) × (68/√1156) × (√961/62)

= (17/34) × (68/34) × (31/62) = 1/2

Q.8.

63 + 83 -73 / 62 + 83 - 72 = ?

A. 287/385 B. 223/167 C. 385/51 D. 231/378

Sol : Option C

63 + 83 -73 / 62 + 83 - 72

=(216+512-343)/(36+64-49)

=(728-343)/(100-49)

=385/51

Q.9.

(19×9+31×10+32×11)/(233.25×2-50) = A. 4 B. 8 C. 6 D. 2

Sol : Option D

(19×9+31×10+32×11)/(233.25×2-50)

=171+310+350/466.5-50

=833/416.5

=2